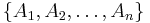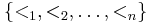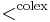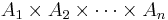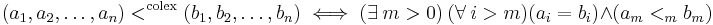Colexicographical order

In mathematics, the colexicographic or colex order, is a natural order structure of the Cartesian product of two or more ordered sets. It is similar in structure to the lexicographical order. Colexicographical ordering is used in the Kruskal-Katona theorem.

Given two partially ordered sets A and B, the colexicographical order on the Cartesian product A × B is defined as

(a,b) ≤ (a′,b′) if and only if b < b′ or (b = b′ and a ≤ a′).

The result is a partial order. If A and B are totally ordered, then the result is a total order also.

More generally, one can define the colexicographic order on the Cartesian product of n ordered sets.

Suppose

\{ A_1, A_2, \ldots, A_n \}

is an n-tuple of sets, with respective total orderings

\{ <_1, <_2, \ldots, <_n \}

The colex ordering

\ \ <^\text{colex}

of

A_1 \times A_2 \times \cdots \times A_n

is then

(a_1, a_2, \dots, a_n) <^\text{colex} (b_1,b_2, \dots, b_n) \iff (\exists\ m > 0) \ (\forall\ i > m) (a_i = b_i) \land (a_m <_m b_m)

The following is an ordering on subsets of size 3 from the set 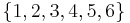\{1,2,3,4,5,6\}, based on the colex ordering of the triples obtained by writing the elements of each subset in ascending order:

123 < 124 < 134 < 234 < 125 < 135 < 235 < 145 < 245 < 345 < 126 < 136 < 236 < 146 < 246 < 346 < 156 < 256 < 356 < 456

External link

Colexicographic order in the OEIS-Wiki